Somut araçlar veya nesneler kullanmak matematiksel gelişimi teşvik etmek açısından önemlidir; ancak çocuklar 10'a kadar saymayı en iyi şekilde nasıl öğrenebilirler?
Çocuklar okula başladıklarında sayıları (“bir, iki, üç…”) okumayı ve yazmayı (1, 2, 3…) öğrenirler. Bu sayıların ne anlama geldiğini öğrenmek daha da zordur ve sayılar birden fazla rakama sahip olduğunda (42 ve 608 gibi) bu daha da karmaşık hale gelir.
Bu tür “çok basamaklı” sayıların anlamının sadece onlara bakarak veya onlarla hesaplamalar yaparak anlaşılamayacağı ortaya çıktı. Sayı sistemimizin şeffaf olmayan pek çok gizli anlamı vardır ve bu da çocukların bunu anlamasını zorlaştırır.
Concordia Üniversitesi Matematik Öğretme ve Öğrenim Laboratuvarı, ilkokul öğretmenleriyle işbirliği içinde, küçük çocukların çok basamaklı sayıları anlamalarını destekleyebilecek araçları araştırıyor.
Somut nesneler kullanmanın (kamışları 10'lu gruplar halinde demetlemek gibi) etkisini araştırıyoruz. Ayrıca sayı çizgileri ve çizelgeleri gibi görsel araçların veya sayıları temsil eden kelimelerin (40 için kullanılan kelime "kırk") ve yazılı gösterimlerin (örneğin, 42) kullanımını da araştırıyoruz.
Sayılar nasıl çalışır?
Son araştırmamız, 1'den 100'e kadar sayıları içeren 10'a 10'luk tablolardan oluşan ve grafikteki her satırın 10'lu gruplar halinde sayılar içerdiği "yüzler tablosunun" çocuklara 10'a kadar saymayı öğretmek için yararlı olup olamayacağını inceledi; bu, anlama için temel bir şeydir.
Bir sayının içinde ne var?
Yetişkinlerin çoğu, 42'deki "4" ve "2" rakamlarının sırasıyla dört onluk ve iki birlik anlamına geldiğini bilir.
Ancak küçük çocuklar sayıları öğrenmeye başladıklarında doğal olarak 10'ları ve 42 gibi bir sayıdaki birleri görmezler. "4" ve "2" rakamlarının anlamını ayırt etmeden sayının birden 42'ye kadar sayılan 42 şeyi temsil ettiğini düşünürler. ” Zamanla sayma ve diğer aktiviteler yoluyla çocuklar dördünü 40'tan oluşan bir koleksiyon olarak görürler .
Ancak bu farkındalık matematikte daha ileri konuların öğrenilmesi için yeterli değildir.
Bir sonraki önemli adım, 42'nin 10 ve iki birden oluşan dört farklı gruptan oluştuğunu ve dört 10'un sanki birmiş gibi sayılabileceğini görmektir (örneğin, 42 bir, iki, üç, dört 10'dur ve bir, iki, “birler”).
Sonuçta sayıları anlamanın en zorlu yönlerinden biri, onlu ve birli grupların farklı türde birimler olmasıdır .
Sayılar farklı şekillerde düzenlenebilir
Yüzlerce çizelgedeki sayılar farklı şekillerde düzenlenebilir. Yukarıdan aşağıya yüzler grafiğinin sol üst köşesinde “1” rakamı, sağ alt köşesinde ise 100 rakamı bulunur.
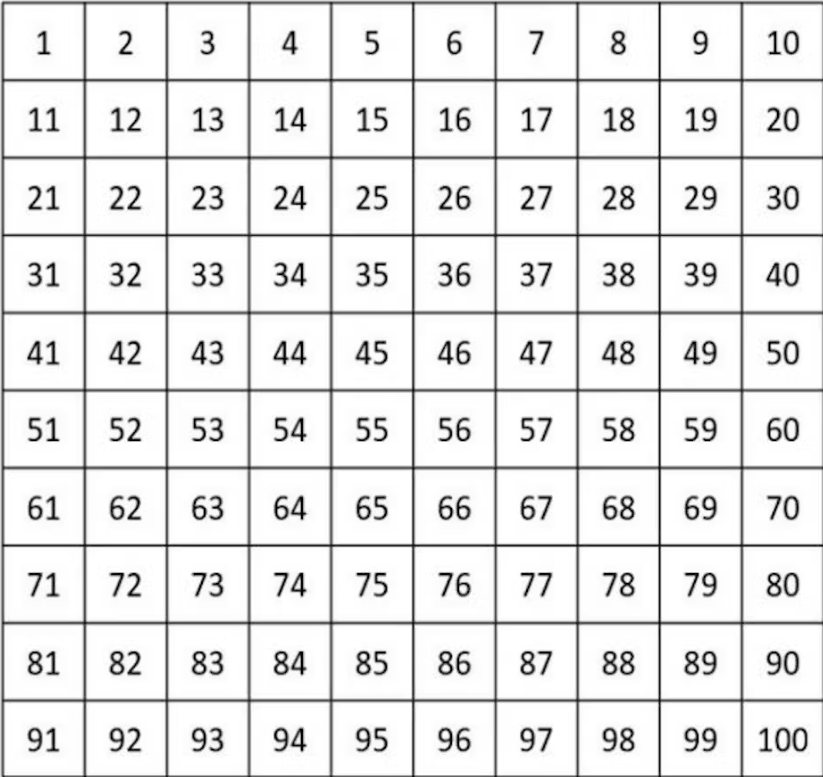
Sayılar her seferinde bir satır aşağıya doğru 10'ar artar, örneğin bir aşağı atlama kullanarak 24'ten 34'e çıkmak gibi. İkinci bir grafik türü, sayıların ters yönde arttığı "aşağıdan yukarıya" grafiktir.
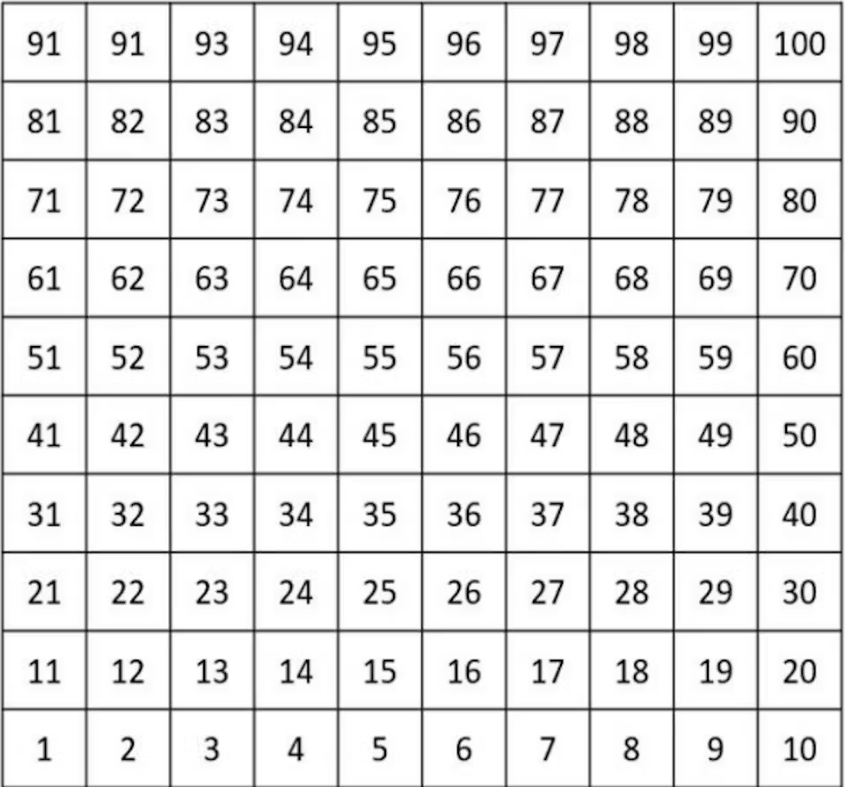
10'ar saniye sayma
Çocuklar problemleri çözmek için çizelgede bir sayıdan diğerine geçebilirler . Örneğin 24 + 20 dikkate alındığında çocuklar 24'ten başlayabilir ve 20 alan hareket ederek 44'e inebilirler.
Başka bir yol da, 44'e gelene kadar iki sıra yukarı (veya grafiğe bağlı olarak aşağı) hareket etmektir (örneğin, "bir", "iki" diye sayarak). Bu ikinci yöntem, çok basamaklı sayıların aşağıdakilerden oluştuğuna dair gelişen bir anlayışı göstermektedir. Sayı sistemine ilişkin ileri düzey bilgi için kritik olan 10'lu farklı gruplar.
Bu hikayenin yazarlarından biri olan Vera Wagner, Concordia Üniversitesi'ndeki yüksek lisans araştırması için, çocukların yukarıya doğru hareket ettikçe sayıların büyüdüğü aşağıdan yukarıya grafikle problemleri çözmeyi daha sezgisel bulabileceklerini düşündü.
Sonuçta bitkiler uzar ve bardak dolduruldukça içindeki sıvı yükselir. Bu tür tanıdık deneyimler nedeniyle çocukların aşağıdan yukarıya grafikte yukarıdan aşağıya tabloya göre onlarca kat daha sık hareket edeceğini düşünüyordu.
Anaokulu öğrencileri ve 1. Sınıf öğrencileriyle çalışma
Bu hipotezi incelemek için Kanada ve Amerika Birleşik Devletleri'ndeki 47 anaokulu ve birinci sınıf öğrencisiyle çalıştık. Evde biri hariç tüm çocuklar İngilizce konuşuyordu. Evde İngilizcenin yanı sıra 14'ü Fransızca, dördü İspanyolca, biri Rusça, biri Arapça, biri Mandarin Çincesi konuşuyordu ve biri de bir dereceye kadar ASL ile iletişim kuruyordu.
Çalışmadaki tüm çocuk katılımcılara, aritmetik kelime problemlerini çözmek için araştırma asistanı André Loiselle tarafından programlanan yukarıdan aşağıya veya aşağıdan yukarıya yüzler tablosunun çevrimiçi bir versiyonunu atadık.
Bulduğumuz şey bizi şaşırttı : Çocuklar yukarıdan aşağıya grafikte aşağıdan yukarıya olana göre onlarca kat daha fazla sayıldı. Bu yapabileceklerini düşündüğümüz şeyin tam tersiydi!
Bu bulgu, yukarıdan aşağıya grafiğin, çocukların sanki birermiş gibi (yani her seferinde bir satır yukarı veya aşağı) onlarca kez saymalarını teşvik ettiğini ve bu onların matematiksel gelişimlerinde önemli bir adım olduğunu göstermektedir. Aşağıdan yukarıya grafiği kullanan çocukların rakamları karıştırma ve yanlış yöne gitme olasılıkları daha yüksekti.
Araçlar öğrenmeyi etkileyebilir
Araştırmamız, matematik sınıfında kullanılan araç türlerinin çocukların öğrenimini farklı şekillerde etkileyebileceğini öne sürüyor.
Yukarıdan aşağıya grafiğin bir avantajı, çocukların çalışmamızdaki okullarda resmi eğitim dilleri olan İngilizce ve Fransızca'da okumayı öğrendikleri yönle eşleşen soldan sağa ve aşağı doğru hareket olabilir. Farklı bir yönde okumayı öğrenen çocuklar (örneğin, Arapça'da olduğu gibi sağdan sola ), ana dili İngilizce veya Fransızca olan çocuklardan bazı matematik araçlarıyla farklı şekilde etkileşime girebilirler.
Matematik öğreniminde kültürel deneyimlerin rolü, sınıf için öğretim araçlarının tasarımı ve kültüre duyarlı matematik öğretiminin uygunluğu hakkında soruların ortaya çıkmasına neden olur. Gelecekteki araştırmalar, okuma yönü ile yüzler tablosunun kullanımı arasındaki ilişkiyi doğrudan incelemeye çalışabilir.











